Which Diagram Shows Lines That Must Be Parallel Lines Cut By A Transversal: Ultimate Guide
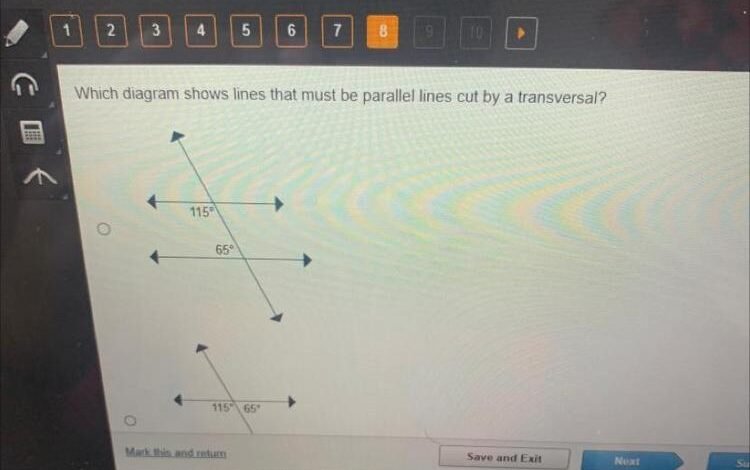
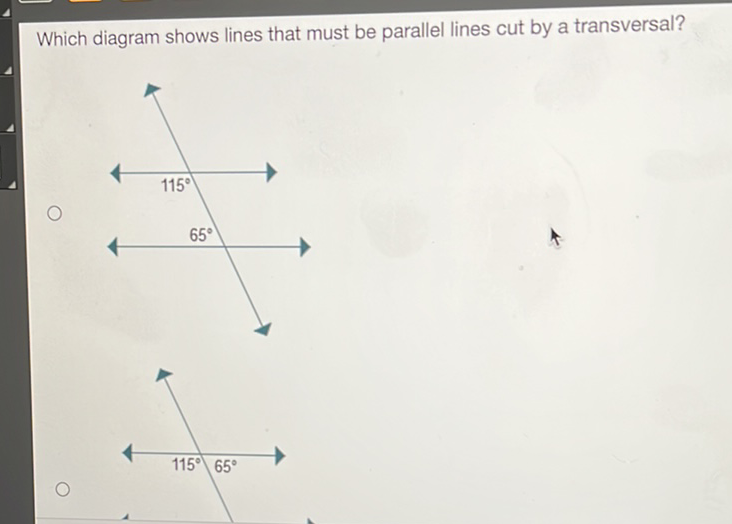
To identify which diagram shows parallel lines cut by a transversal, you need to understand a few key concepts. Parallel lines are lines that never meet, no matter how far they extend.
A transversal is a line that crosses two or more lines at distinct points. In geometry, recognizing parallel lines cut by a transversal can help solve various problems. These diagrams often show angles formed by the intersection. Certain angle pairs, like corresponding angles and alternate interior angles, can indicate parallel lines.
By understanding these relationships, you can easily spot parallel lines in any diagram. This knowledge is not only crucial for solving math problems but also useful in real-life applications, such as architecture and design. Let’s dive deeper into the details and learn how to identify these lines with confidence.

Credit: brainly.com
Introduction To Parallel Lines And Transversals
Understanding parallel lines and transversals is essential in geometry. These concepts are foundational. They help in solving various geometric problems. Let’s dive into the details.
Importance Of Parallel Lines
Parallel lines never meet. They are always equidistant. This makes them unique. In geometry, they simplify complex problems. Architects use them to design buildings. Engineers rely on them for accurate measurements. Without parallel lines, many designs would fail.
Role Of A Transversal
A transversal is a line that crosses two or more lines. It creates angles. These angles have special properties. Identifying these angles helps solve geometric problems. Transversals are crucial in understanding parallel lines. They are used in various fields. For example, in navigation and mapping. Knowing how transversals work can make geometry easier.
Identifying Parallel Lines
Understanding parallel lines is essential in geometry. Parallel lines are lines that never meet. They stay the same distance apart. Knowing this can help you solve many geometric problems.
Basic Characteristics
Parallel lines have unique characteristics:
- They have the same slope.
- They never intersect.
- They are equidistant at all points.
These features help in identifying parallel lines. Look for these traits in diagrams.
Visual Clues
To spot parallel lines, look for:
- Transversal Lines: A line that crosses two or more lines.
- Corresponding Angles: Angles in matching corners.
- Alternate Interior Angles: Angles on opposite sides of the transversal.
- Alternate Exterior Angles: Angles outside the parallel lines, on opposite sides.
These clues can help you identify if lines are parallel. Let’s see a table to summarize these:
| Clue | Description |
|---|---|
| Transversal Lines | A line crossing two or more lines |
| Corresponding Angles | Angles in matching corners |
| Alternate Interior Angles | Angles on opposite sides of the transversal, inside the parallel lines |
| Alternate Exterior Angles | Angles on opposite sides of the transversal, outside the parallel lines |
Using these clues makes it easier to spot parallel lines. Practice will enhance your skills.
Transversals And Their Properties
A diagram with two lines cut by a transversal, showing equal corresponding angles, indicates parallel lines. Identifying parallel lines involves checking if alternate interior angles are equal.
Understanding transversals and their properties is essential in geometry. Transversals intersect parallel lines and form various angles. Knowing these properties helps in identifying parallel lines and solving geometric problems.Definition Of A Transversal
A transversal is a line that crosses at least two other lines. When it intersects two parallel lines, it creates specific angles. These angles have unique properties useful in geometry.Types Of Angles Formed
Transversals create several types of angles. They include corresponding angles, alternate interior angles, and alternate exterior angles. Each type has distinct properties. Corresponding angles are on the same side of the transversal. They are equal when the lines are parallel. Alternate interior angles lie between the two lines. They are on opposite sides of the transversal. These angles are equal if the lines are parallel. Alternate exterior angles are outside the two lines. Like alternate interior angles, they are equal if the lines are parallel. Understanding these angles helps in identifying parallel lines. It also aids in solving complex geometric problems. Identifying and using these angles can simplify many calculations. “`Key Angle Relationships
Understanding key angle relationships is essential to identifying parallel lines cut by a transversal. These angles help determine if the lines are indeed parallel. Let’s explore some of the key angle relationships found in these scenarios.
Corresponding Angles
Corresponding angles are pairs of angles that are in similar positions at each intersection. They lie on the same side of the transversal. If the corresponding angles are equal, the lines are parallel.
Alternate Interior Angles
Alternate interior angles are located between the two lines but on opposite sides of the transversal. If these angles are congruent, the lines are parallel.
Alternate Exterior Angles
Alternate exterior angles are found outside the two lines and on opposite sides of the transversal. If these angles are equal, the lines are parallel.
Consecutive Interior Angles
Consecutive interior angles are on the same side of the transversal and between the two lines. If the sum of these angles is 180 degrees, the lines are parallel.
Using Diagrams To Identify Parallel Lines
Using diagrams is a powerful way to identify parallel lines cut by a transversal. These visuals help in understanding complex geometry concepts. They make it easier to spot which lines are parallel.
Common Diagram Types
There are several diagram types to identify parallel lines. The most common ones include:
- Two lines with a transversal cutting through.
- Parallel line indicators like arrows or double lines.
- Angles formed by the transversal, such as alternate interior angles.
Each of these diagrams serves a specific purpose. They help in recognizing and proving parallel lines.
Steps To Analyze A Diagram
Follow these simple steps to analyze a diagram:
- First, identify the lines cut by the transversal.
- Next, look for angle relationships. Check for corresponding or alternate interior angles.
- Then, look for parallel line indicators like arrows or special markings.
- Finally, use geometric rules to confirm parallel lines. If the angle relationships match, the lines are parallel.
These steps make it easy to use diagrams for identifying parallel lines.
Common Mistakes And Misconceptions
Understanding which diagram shows lines that must be parallel lines cut by a transversal can be tricky. Many students and even adults make common mistakes and have misconceptions. These errors can lead to wrong answers and confusion.
Misinterpreting Angles
Misinterpreting angles is a common mistake. People often think that any equal angles mean the lines are parallel. This is not always true. Only specific angle pairs indicate parallel lines. These include corresponding angles, alternate interior angles, and alternate exterior angles.
It is crucial to identify these angles correctly. Mistakes happen when people confuse these with other types of angles. Practice and careful observation help avoid this error.
Ignoring Angle Sum
Ignoring the angle sum is another common misconception. Some people forget that the sum of angles on a straight line is 180 degrees. This rule helps in identifying parallel lines. If two angles add up to 180 degrees, the lines might be parallel.
Remembering this simple rule can make a big difference. It helps in checking if the lines are truly parallel. Always double-check your angle sums to avoid mistakes.
Practice Problems
Practice problems are essential for mastering the identification of parallel lines cut by a transversal. They help reinforce concepts and improve problem-solving skills. Let’s dive into some practice problems.
Simple Identification
Start with basic diagrams to identify parallel lines. Look for alternate interior angles and corresponding angles that are equal. Here’s an example:
| Diagram | Identification |
|---|---|
 |
Lines AB and CD are parallel if angles 1 and 2 are equal. |
 |
Lines EF and GH are parallel if angles 3 and 4 are corresponding angles. |
Complex Scenarios
Practice with more complex diagrams. Identify multiple sets of parallel lines. Here’s an example:
- Observe each pair of alternate interior angles.
- Check the corresponding angles.
- Ensure consecutive interior angles are supplementary.
Consider this diagram:

- Lines AB and CD are parallel if angle 1 equals angle 2.
- Lines EF and GH are parallel if angle 3 equals angle 4.
- Lines IJ and KL are parallel if angle 5 equals angle 6.
Use these steps to practice and master the identification of parallel lines cut by a transversal.

Credit: brainly.com
Advanced Concepts
Understanding which diagram shows lines that must be parallel lines cut by a transversal can be complex. This section explores advanced concepts in this topic. It delves into non-Euclidean geometry and real-world applications. These insights will enhance your comprehension of parallel lines and transversals.
Non-euclidean Geometry
Non-Euclidean geometry challenges our usual understanding of parallel lines. In this geometry, parallel lines can behave differently. For instance, in hyperbolic geometry, parallel lines may diverge. In spherical geometry, lines can intersect multiple times. These concepts show that parallel lines are not always straightforward.
Understanding non-Euclidean geometry deepens our grasp of mathematical principles. It reveals the diversity of geometric concepts. This knowledge is valuable for advanced studies in mathematics. It also helps in understanding different models of the universe.
Real-world Applications
Parallel lines and transversals have many real-world applications. For example, in architecture, ensuring walls are parallel is crucial. This ensures stability and aesthetic appeal. Engineers use these principles in designing roads and bridges. Accurate parallel lines ensure safety and efficiency.
In art, parallel lines create perspective and depth. Artists use these concepts to make their work realistic. Understanding these principles enhances both technical and creative fields. It shows the practical importance of parallel lines and transversals in everyday life.
Credit: www.airmath.com
Frequently Asked Questions
What Is A Transversal Line?
A transversal line is a line that intersects two or more other lines at distinct points. When it crosses parallel lines, it forms various angles.
How Do You Identify Parallel Lines?
Parallel lines are equidistant and never meet. In diagrams, they are often marked with arrow symbols or can be identified using angle relationships.
What Are Corresponding Angles?
Corresponding angles are pairs of angles that occupy the same relative position at each intersection where a transversal crosses parallel lines. These angles are equal.
Why Are Alternate Interior Angles Important?
Alternate interior angles are equal when a transversal crosses parallel lines. This property helps in proving that the lines are parallel.
Conclusion
Understanding parallel lines cut by a transversal is crucial in geometry. Identifying these diagrams helps with various math problems. Always look for matching angles. Check for equal corresponding angles or alternate interior angles. This knowledge simplifies complex geometric concepts. Practice often to improve your skills.
Remember, geometry requires observation and practice. Keep learning, and you’ll get better. Thank you for reading!



